AC 自动机
从功能上来说,AC 自动机是可以求解多个小串 在长串 的中是否出现过、出现的次数和每一次出现的位置。从具体实现上来说,AC 自动机就是在 trie 树上跑 KMP。其时间复杂度为线性的,是 。
AC 自动机的失配指针与 KMP 的 border 数组极为相似,可以参考理解。如果节点 的失配指针为 ,那么从根节点到 的边上的字符形成的字符串应该与从 出发向根节点行进 步到达的点 再从 走到 边上的字符形成的字符串一样,在满足 的前提下,应该使 尽可能的大。
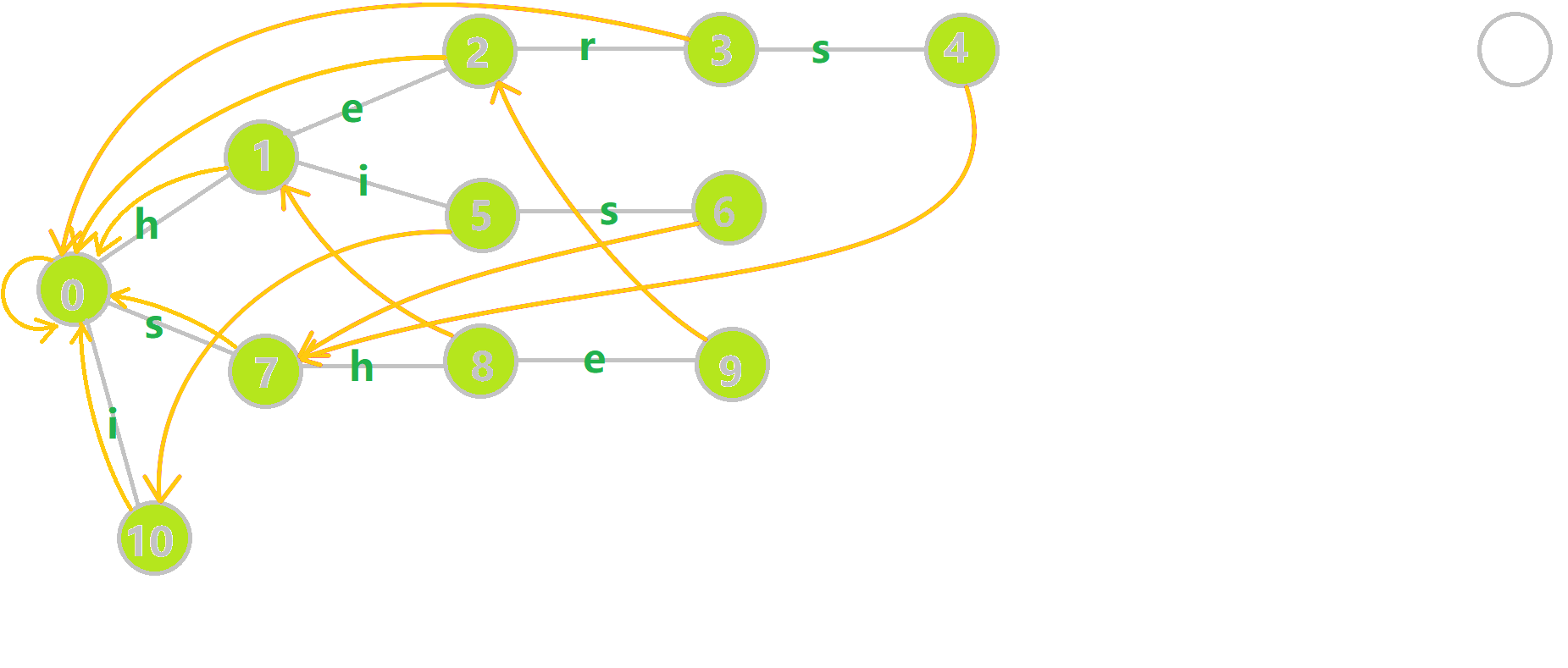
对于上图, 号节点的失配指针之所以是 是因为从根节点到 好节点边上的字符串 与从 号节点到 好节点边上的字符串 是一样的。
我们对数组进行一些定义,我们约定 表示 的失配指针, 表示在 后添加 最终到达的地方, 表示树边。
那么在统计的时候会出现一个问题,因为我们维护的是最长的满足要求的位置,例如我们询问的串是 而我们找到最长的匹配的其实 。
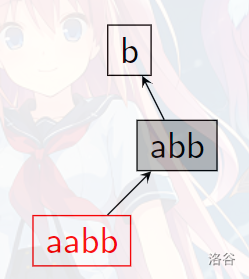
其中箭头表示的 指针,容易理解如果某个节点 被经过那么就代表 的这个字符串出现了一次。
而因为 出现了 也一定出现了,同理 也一定出现了,所以我们把 中所有 树的祖先全部标记一遍出现了一次。
因为该所有祖先然后单点查等价于你进行单点该然后子树查,所以我们直接把树拍成一个 dfs 序然后就可以用 RMQ 在线维护就行了。
需要理解如果 是某一个 的前缀,那么经过 并不意味着 出现了,需要区分。
